Math Mondays-Factoring

Financial Fridays-Fastweb Edition

https://www.fastweb.com/financial-aid/articles/top-strategies-for-maximizing-aid-eligibility

Something to Think About...

Why do you think diversity is important in higher education?

Wisdom Wednesday

Teaching Tuesdays-MLA Format

Math Mondays: Quadratic Formula

Financial Literacy: College Edition

Do you know many students aren't aware of the total cost a 4-year education? Many go to school without the proper information on how to apply for loans, the interest rate on loans, and what it means to borrow loans from private companies. Check out this article to see how many students inevitably fall into the trap of student debt.
https://www.fastweb.com/financial-aid/articles/guide-to-student-loans

School's and Creativity: TedTalk to Consider

Thursday Thought of the Day

Why do you think people are more likely to trust word of mouth rather than ads on Television?

Wisdom Wednesdays-Kofi Annan

"Knowledge is power. Information is liberating. Education is the premise of progress, in every society, in every family."-Kofi Annan

Teaching Tuesdays-Punctuation Matters!

Punctuation

These OWL resources will help you with punctuation, such as using commas, quotation marks, apostrophes, and hyphens.

Punctuation

When speaking, we can pause or change the tone of our voices to indicate emphasis. When writing, we must use punctuation to indicate these places of emphasis. This resource should help to clarify when and how to use various marks of punctuation.

Sentence Punctuation Patterns

This handout describes eight sentence punctuation patterns with examples.

Independent and Dependent Clauses

This handout defines dependent and independent clauses and explores how they are treated in standard usage.

Conquering the Comma

This presentation is designed to acquaint your students with the rules of comma usage, including placement in compound sentences, after introductory elements, with dependent phrases and clauses, around nonessential elements, in a series, and with adjectives. This presentation will also cover methods for avoiding a common comma error—the comma splice. The thirty-one slide presentation included here is designed to aid the facilitator in an interactive presentation of the elements of comma usage. This presentation is ideal for the beginning of a composition course, the assignment of a writing project, or as a refresher presentation for grammar usage.

Commas

This resource offers a number of pages about comma use.

Apostrophe

This handout provides rules and examples for apostrophe usage.

Hyphens

A comprehensive rundown on the proper use of the hyphen.

Quotation Marks

https://owl.english.purdue.edu/owl/section/1/6/

A rundown of the general rules of when and where to use quotation marks.

Math Mondays:Fractions

Reducing Fractions

Mixed & Improper FractionsMultiplying & DividingAdding & SubtractingPolynomial Fractions

Purplemath

In what follows, it will sometimes be useful to remember that fractions can indicate division. For instance, 1/3 can mean "one divided by three", as well as "one part out of three parts". In fact, let's cut to the chase; memorize this sentence: "Fractions are division."

You know that any number, divided by itself, is just 1. You use this fact when you reduce fractions. If you can convert part of a given fraction into being a multiplied form of 1, then you can ignore this part, because multiplying by 1 doesn't change anying.

MathHelp.com

Reducing Fractions to Lowest Terms

For instance, here's how you would find and use a form of 1 to reduce 4/8:

$\dfrac{4}{8} = \dfrac{1 \cdot 4}{2 \cdot 4} = \dfrac{1}{2} \cdot \dfrac{4}{4} = \dfrac{1}{2} \cdot 1 = \dfrac{1}{2}$

To be very clear, the point of finding the common factor (in this case, the 4's) is to allow you to convert part of the fraction to 1. Since 4/4 = 1, then what I did above was the following:

---

Advertisement

Warning: Note how I switched from a fraction with products (in the numerator and denominator):

$\dfrac{1 \cdot 4}{2 \cdot 4}$

...to a product of fractions:

$\dfrac{1}{2} \cdot \dfrac{4}{4}$

This switch is okay as long as you're multiplying:

$\dfrac{1 \cdot 4}{2 \cdot 4} = \dfrac{1}{2} \cdot \dfrac{4}{4}$

...but it is very much NOT if you're adding. For instance:

$\dfrac{1 + 4}{2 + 4} \neq \dfrac{1}{2} + \dfrac{4}{4}$

The left-hand side above, being a fraction containing addition, is equal to 5/6, while the right-hand side above, being an addition containing fractions, is equal to 1 1/2, so the two expressions are not at all the same value. Just remember: For fractions, multiplying is way easier than adding. Now, to get back to business...

---

Content Continues Below

---

In addition to the canceling method I used above (with the pink 1's), you may also have seen either of the following "shorthands" for cancellation:

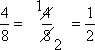
Any of these formats is fine. The last two are probably simplest for your handwritten homework; the first one is easier for typesetting.

---

If you have a regular (scientific, business, etc.) calculator that can handle fractions, then you can enter the fraction and then hit the "equals" button to get the reduced fraction. If you have a graphing calculator with a fraction command, then you can enter the fraction as a division (because 4/8 means "four divided by eight"), and then convert to fraction form. Check your manual.

If your calculator can't handle fractions, or if the denominator is too large for the calculator to handle, here's how you do the reduction by hand.

• Reduce $\mathbf{\color{green}{\dfrac{2940}{3150}}}$ to simplest form.

I'll grab my calculator and some scrap paper, and factor the numerator (top number) and denominator (bottom number). A quick shorthand for getting the prime factorization of each of these numbers is demonstrated below, in the stacked division (by prime numbers) of 2940:

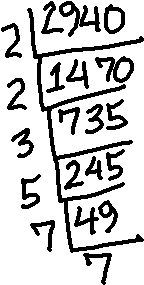
To find the factorization, I just read off the prime factors from around the outside of the upside-down division. From the above, I can see that 2940 factors as 2×2×3×5×7×7.

Affiliate

Next, I'll factor the denominator, being the number 3150:

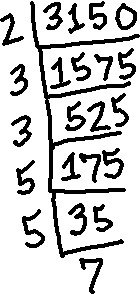
So 3150 factors as 2×3×3×5×5×7.

Now I can reduce the fraction by canceling off the common factors:

---

The next section reviews mixed numbers and improper (or "vulgar") fractions....http://www.purplemath.com/modules/fraction.htm

Financial Fridays-Balancing a Checkbook

http://financeintheclassroom.org/downloads/CheckingUnitLessonPlans.pdf

Click on the link to learn how to balance a checkbook! After reading through the content, practice the problems.

Thursday Thoughts: What makes a person sucessful?

Success can be defined in a variety of ways: through work, school, or family but what makes an individual successful?

Words of Wisdom-Quote by Malcolm X

Teaching Tuesdays: How to Quote

Extended Rules for Using Quotation Marks

Summary:

A rundown of the general rules of when and where to use quotation marks.

Contributors:Sean M. Conrey, Mark Pepper, Allen Brizee
Last Edited: 2010-04-17 06:03:37

Altering the Source Material in a Quotation

The responsibility of representing other people's words accurately lies firmly on the shoulders of the author. Inaccurate quotes not only defeat the purpose of using a quote, they may also constitute plagiarism. However, there are approved methods for altering quotes for either clarity or succinctness.

Quote length

If the original quote is too long and you feel not all the words are necessary in your own paper, you may omit part of the quote. Replace the missing words with an ellipsis.

Original Quote: The quarterback told the reporter, "It's quite simple. They played a better game, scored more points, and that's why we lost."

Omitted Material: The quarterback told the reporter, "It's quite simple. They . . . scored more points, and that's why we lost."

Make sure that the words you remove do not alter the basic meaning of the original quote in any way. Also ensure that the quote's integration and missing material still leave a grammatically correct sentence.

Quote context

If the context of your quote might be unclear, you may add a few words to provide clarity. Enclose the added material in brackets.

Added Material: The quarterback told the reporter, "It's quite simple. They [the other team] played a better game, scored more points, and that's why we lost."

Quotations within a Quotation

Use single quotation marks to enclose quotes within another quotation.

The reporter told me, "When I interviewed the quarterback, he said they simply 'played a better game.'"

Quotation Marks Beyond Quoting

Quotation marks may additionally be used to indicate words used ironically or with some reservation.

The great march of "progress" has left millions impoverished and hungry.

Do not use quotation marks for words used as words themselves. In this case, you should use italics.

The English word nuance comes from a Middle French word meaning "shades of color."https://owl.english.purdue.edu/owl/resource/577/02/

Math Monday-Factoring Numbers

Factoring Numbers

Purplemath

"Factors" are the numbers you multiply to get another number. For instance, factors of 15 are 3 and 5, because 3×5 = 15. Some numbers have more than one factorization (more than one way of being factored). For instance, 12 can be factored as 1×12, 2×6, or 3×4. A number that can only be factored as 1 times itself is called "prime". The first few primes are 2, 3, 5, 7, 11, and 13. The number 1 is not regarded as a prime, and is usually not included in factorizations, because 1 goes into everything. (The number 1 is a bit boring in this context, so it gets ignored.)

MathHelp.com

Factoring Numbers: Prime Factorization

You most often want to find the "prime factorization" of a number: the list of all the prime-number factors of a given number. The prime factorization does not include 1, but does include every copy of every prime factor. For instance, the prime factorization of 8 is 2×2×2, not just "2". Yes, 2 is the only factor, but you need three copies of it to multiply back to 8, so the prime factorization includes all three copies.

On the other hand, the prime factorization includes ONLY the prime factors, not any products of those factors. For instance, even though 2×2 = 4, and even though 4 is a divisor of 8, 4 is NOT in the PRIME factorization of 8. That is because 8 does NOT equal 2×2×2×4! This accidental over-duplication of factors is another reason why the prime factorization is often best: it avoids counting any factor too many times. Suppose that you need to find the prime factorization of 24. Sometimes a student will just list all the divisors of 24: 1, 2, 3, 4, 6, 8, 12, and 24. Then the student will do something like make the product of all these divisors: 1×2×3×4×6×8×12×24. But this equals 331776, not 24. So it's best to stick to the prime factorization, even if the problem doesn't require it, in order to avoid either omitting a factor or else over-duplicating one.

In the case of 24, you can find the prime factorization by taking 24 and dividing it by the smallest prime number that goes into 24: 24 ÷ 2 = 12. (Actually, the "smallest" part is not as important as the "prime" part; the "smallest" part is mostly to make your work easier, because dividing by smaller numbers is simpler.) Now divide out the smallest number that goes into 12: 12 ÷ 2 = 6. Now divide out the smallest number that goes into 6: 6 ÷ 2 = 3. Since 3 is prime, you're done factoring, and the prime factorization is 2×2×2×3.

Advertisement

An easy way of keeping track of the factorization is to do upside-down division. It looks like this:

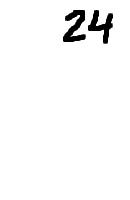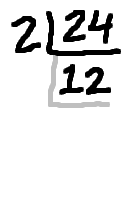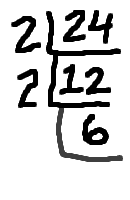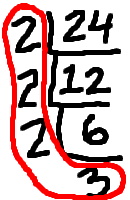
The nice thing about this upside-down division is that, when you're done, the prime factorization is the product of all the numbers around the outside. The factors are circled in red above. By the way, this upside-down division is something that should probably be done on scratch-paper, and not handed in as part of your homework.

• Find the prime factorization of 1050.

I'll do the upside-down division:

Then my answer is: 1050 = 2 × 3 × 5 × 5 × 7

Some texts prefer that answers such as this be written using exponential notation, in which case the final answer would be written as 2×3×52×7.

You can do the repeated division "right-side up", too, if you prefer. The process works the same way, but the division is reversed in orientation. The above problem would be worked out like this:

• Find the prime factorization of 1092.

I'll do the repeated division:

1092 = 2 × 2 × 3 × 7 × 13

This answer might also be written as 22×3×7×13.

---

Content Continues Below

---

By the way, there are some divisibility rules that can help you find the numbers to divide by. There are many divisibility rules, but the simplest to use are these:

If the number is even, then it's divisible by 2.

If the number's digits sum to a number that's divisible by 3, then the number itself is divisible by 3.

If the number ends with a 0 or a 5, then it's divisible by 5.

Of course, if the number is divisible twice by 2, then it's divisible by 4; if it's divisible by 2 and by 3, then it's divisible by 6; and if it's divisible twice by 3 (or if the sum of the digits is divisible by 9), then it's divisible by 9. But since you're finding the prime factorization, you don't really care about these non-prime divisibility rules. There is a rule for divisibility by 7, but it's complicated enough that it's probably easier to just do the division on your calculator and see if it comes out even.

If you run out of small primes and you're not done factoring, then keep trying bigger and bigger primes (11, 13, 17, 19, 23, etc) until you find something that works – or until you reach primes whose squares are bigger than what you're dividing into. Why? If your prime doesn't divide in, then the only potential divisors are bigger primes. Since the square of your prime is bigger than the number, then a bigger prime must have as its remainder a smaller number than your prime. The only smaller number left, since all the smaller primes have been eliminated, is 1. So the number left must be prime, and you're done.

---

You can use the Mathway widget below to practice finding the prime factorization. Try the entered exercise, or type in your own exercise. Then click the button to compare your answer to Mathway's.