Math Mondays: Least Common Factor

Financial Fridays-Free Application for Student Financial Aid

What's the FAFSA? And Why You Should Care

Completing the FAFSA will help you earn federal financial aid.

By The Fastweb Team

August 17, 2017

You must submit the Free Application for Federal Student Aid (FAFSA) if you want to apply for federal and state financial aid. Many colleges and universities, especially public institutions, also require the FAFSA. You must submit the FAFSA every year that you want aid.

Obtaining a FAFSA

The FAFSA is available in several formats, including online, PDF and paper versions.

The best option is to complete the web-based version of the FAFSA at www.fafsa.ed.gov, known as FAFSA on the Web. It includes step-by-step instructions for completing the online FAFSA as well as preapplication worksheets. You can obtain a PIN to electronically sign the form by visiting www.pin.ed.gov. If you have technical questions about using FAFSA on the Web, call 1-800-4-FED-AID.

FAFSA on the Web offers several benefits, including:

• You will get your Student Aid Report (SAR) sooner than with the paper or PDF forms.


• Your FAFSA will be more accurate, since the FAFSA on the Web has built-in edit checks to catch simple errors and you avoid errors introduced by the OCR process.


• You will save the federal government money by reducing their processing costs.


• The online FAFSA allows you to list up to ten colleges, while the paper FAFSA has space only for four colleges.

Most families complete the FAFSA online these days.

Paper versions are no longer bulk-distributed to high schools, colleges and libraries, with a few exceptions. (The exceptions involve organizations that work with underrepresented populations and students that do not have access to the Internet or a phone.) However, students may obtain up to three copies of the paper version by calling 1-800-4-FED-AID(1-800-433-3242) or 1-391-337-5665. (Hearing impaired individuals should call the TTYnumber 1-800-730-8913.) Paper FAFSAs can be ordered starting November 1 of each year.

Note that the FAFSA may not be submitted before October 1, even if the paper and PDFversions are available sooner.

EFC Calculators

FinAid’s Financial Aid Estimation Form may be used to calculate your EFC and an estimate of your eligibility for financial aid. This may help you understand a bit about how the federal need analysis system works. You can also run “what-if” experiments to see how much aid you’ll get under various scenarios. FinAid also has a QuickEFC calculator that uses much fewer questions to yield a ballpark estimate of your EFC.

Like FinAid’s EFC calculator, the US Department of Education’s FAFSA4CASTER tool also provides an early estimate of financial aid eligible. It is similar to FAFSA on the Web, but omits a handful of questions (e.g., drug conviction, selective service, parent education level, list of colleges, signatures). The FinAid tool provides more detailed analysis and more detailed aid eligibility information, but FAFSA4CASTER will potentially be linked with FAFSA on the Web for prefilling the answers to some of the FAFSA questions.

https://www.fastweb.com/financial-aid/articles/what-s-the-fafsa-and-why-you-should-care

Thursday Thought

Why is diversity important in an outside the classroom?

Wisdom Wednesdays

Teaching Tuesdays-Run on Sentences

Run-On Sentences

A run-on sentence occurs when two or more independent clauses (also known as complete sentences) are connected improperly.

Example: I love to write papers I would write one every day if I had the time.

There are two complete sentences in the above example:

Sentence 1: I love to write papers.

Sentence 2: I would write one every day if I had the time.

---

One common type of run-on sentence is a comma splice. A comma splice occurs when two independent clauses are joined with just a comma.

Example of a comma splice: Participants could leave the study at any time, they needed to indicate their preference.

Sentence 1: Participants could leave the study at any time.

Sentence 2: They needed to indicate their preference.

Some comma splices occur when a writer attempts to use a transitional expression in the middle of a sentence.

Example of a comma splice: The results of the study were inconclusive, therefore more research needs to be done on the topic.

Sentence 1: The results of the study were inconclusive

Transitional expression (conjunctive adverb): therefore

Sentence 2: More research needs to be done on the topic

To fix this type of comma splice, use a semicolon before the transitional expression and add a comma after it. See more examples of this on the semicolon page.

Revision: The results of the study were inconclusive; therefore, more research needs to be done on the topichttp://academicguides.waldenu.edu/writingcenter/grammar/runonsentences.

Math Monday-Geometric Formula Review

Geometric Formula Review

Purplemath

There are many geometric formulas, and they relate height, width, length, or radius, etc, to perimeter, area, surface area, or volume, etc. Some of the formulas are rather complicated, and you hardly ever see them, let alone use them. But there are some basic formulas that you really should memorize, because it really is reasonable for your instructor to expect you to know them.

For instance, it is very easy to find the area A of a rectangle: it is just the length l times the width w:

Arect = lw

MathHelp.com

The "rect" in the formula above is a subscript, indicating that the area "A" being found is that of a rectangle. Because I'm going to be discussing area, volume, etc, formulas for different shapes, I'm using the subscripts to make clear the shape to which the particular formula refers (while using "A" for "area", "SA" for "surface area", "P" for "perimeter", and "V" for "volume"). Subscripting of this sort can be a useful technique for making your meaning clear, so try to keep this in the back of your mind for possible future use.

If you look at a picture of a rectangle, and remember that "perimeter" means "length around the outside", you'll see that a rectangle's perimeter P is the sum of the top and bottom lengths l and the left and right widths w:

Prect = 2l + 2w

Squares are even simpler, because their lengths and widths are identical. The area A and perimeter P of a square with side-length s are given by:

Asqr = s2

Psqr = 4s

You should know the formula for the area of a triangle; it's easy to memorize, and it tends to pop up unexpectedly in the middle of word problems. Given the measurements for the base b and the height h of the triangle, the area Aof the triangle is:

$A_{\text{tri}} = \dfrac{1}{2} bh$

Of course, the perimeter P of the triangle will just be the sum of the lengths of the triangle's three sides.

---

You should know the formula for the circumference C and area A of a circle, given the radius r:

Acir = πr2

Ccir = 2πr

("π" is the number approximated by 3.14159 or the fraction 22/7)

Remember that the radius of a circle is the distance from the center to the outside of a circle. In other words, the radius is just halfway across. If they give you the length of the diameter, being the length of a line through the middle going all the way across the circle, then you'll first have to divide that value in half in order to apply the above formulas.

---

Content Continues Below

---

The above are all "flat", two-dimensional shapes. Sometimes you will have to deal with three-dimensional shapes, such as cubes or cones. For these kinds of shapes, you'll be finding the surface area (if you were painting the object, this is the area that you'd have to cover) and the volume (being the interior space that you could fill, were the shape hollow).

The formula for the volume V of a cube is easy, since the length, the width, and the height are all the same value s:

Vcube = s3

The formula for the surface area (the area you would measure if you needed to paint the ouside of the cube) is fairly easy, too, since all the sides have the same square area of s2. There are six sides (top, bottom, left, right, front, and back), so the surface area SA is:

SAcube= 6s2

The formulas get a bit more complicated for a "rectangular prism", which is the technical term for a brick. The volume V is still fairly simple, being length times width times height:

Vrect = lwh

The surface area formula is a bit more ornate. (Try to follow the reasoning that I'm going to use, because you'll probably forget the formula, but it's easy to recreate if you just take a little time and think about it.) The top and bottom of the "brick" have the same area, being length times width. The left and right sides of the brick have the same area, being width times height. And the front and back of the brick have the same area, being length times height. (Draw a picture, labelling the dimensions, if you're not sure of this.) Then the formula for the surface area SA of a brick is:

SArect= 2lw + 2wh + 2lh

Advertisement

Cylinders (which are like tubes, but with caps on the ends) also come up occasionally. The volume V of a cylinder is easy: it's the area of the end (which is just the area of the circle) times the height h:

Vcyl = πr2h

The surface area SA is the area of the ends (which are just circles), plus the area of the side, which is a circle's circumference times the height h of the cylinder:

SAcyl = 2πr2 + 2πrh

Depending on the class you're taking, you might also need to know the formula for the volume V of a cone with base radius r and height h:

$V_{\text{cone}} = \dfrac{1}{3} \pi r^2$

...or the volume V of a sphere (a ball) with radius r:

$V_{\text{sph}} = \dfrac{4}{3} \pi r^3$

You may notice other formulas cropping up in your homework or classroom exercises. You may need to memorize these other formulas (there are many!), so be sure to check with your instructor before the test to learn which you will be expected to know.

Financial Friday

https://www.fastweb.com/content/fafsa

Thursday Throught

"Life can only be understood backward, but it must be lived forward"-Soren Kierkegaard

What do you think this quote means? How can you apply the quote's message to your daily life?

Words of Wisdom

"The more you use, the more brain you will have to use"-George A. Dorsey

Teaching Tuesdays-How to use a Dash in a sentence

http://www.sussex.ac.uk/informatics/punctuation/hyphenanddash/dash

Math Mondays

Read through the example of how to solve investment problems and solve for the example at the bottom.

Financial Fridays

http://www.richdad.com/Resources/Rich-Dad-Financial-Education-Blog/August-2012/what-is-financial-literacy.aspx

Thursday Thought

Do you believe the heavy financial impact of education has affected students' and their families?

Words of Wisdom

Teaching Tuesday 11 Rules of Grammar

11 Rules of Grammar

Math Mondays-Factoring

Financial Fridays-Fastweb Edition

https://www.fastweb.com/financial-aid/articles/top-strategies-for-maximizing-aid-eligibility

Something to Think About...

Why do you think diversity is important in higher education?

Wisdom Wednesday

Teaching Tuesdays-MLA Format

Math Mondays: Quadratic Formula

Financial Literacy: College Edition

Do you know many students aren't aware of the total cost a 4-year education? Many go to school without the proper information on how to apply for loans, the interest rate on loans, and what it means to borrow loans from private companies. Check out this article to see how many students inevitably fall into the trap of student debt.
https://www.fastweb.com/financial-aid/articles/guide-to-student-loans

School's and Creativity: TedTalk to Consider

Thursday Thought of the Day

Why do you think people are more likely to trust word of mouth rather than ads on Television?

Wisdom Wednesdays-Kofi Annan

"Knowledge is power. Information is liberating. Education is the premise of progress, in every society, in every family."-Kofi Annan

Teaching Tuesdays-Punctuation Matters!

Punctuation

These OWL resources will help you with punctuation, such as using commas, quotation marks, apostrophes, and hyphens.

Punctuation

When speaking, we can pause or change the tone of our voices to indicate emphasis. When writing, we must use punctuation to indicate these places of emphasis. This resource should help to clarify when and how to use various marks of punctuation.

Sentence Punctuation Patterns

This handout describes eight sentence punctuation patterns with examples.

Independent and Dependent Clauses

This handout defines dependent and independent clauses and explores how they are treated in standard usage.

Conquering the Comma

This presentation is designed to acquaint your students with the rules of comma usage, including placement in compound sentences, after introductory elements, with dependent phrases and clauses, around nonessential elements, in a series, and with adjectives. This presentation will also cover methods for avoiding a common comma error—the comma splice. The thirty-one slide presentation included here is designed to aid the facilitator in an interactive presentation of the elements of comma usage. This presentation is ideal for the beginning of a composition course, the assignment of a writing project, or as a refresher presentation for grammar usage.

Commas

This resource offers a number of pages about comma use.

Apostrophe

This handout provides rules and examples for apostrophe usage.

Hyphens

A comprehensive rundown on the proper use of the hyphen.

Quotation Marks

https://owl.english.purdue.edu/owl/section/1/6/

A rundown of the general rules of when and where to use quotation marks.

Math Mondays:Fractions

Reducing Fractions

Mixed & Improper FractionsMultiplying & DividingAdding & SubtractingPolynomial Fractions

Purplemath

In what follows, it will sometimes be useful to remember that fractions can indicate division. For instance, 1/3 can mean "one divided by three", as well as "one part out of three parts". In fact, let's cut to the chase; memorize this sentence: "Fractions are division."

You know that any number, divided by itself, is just 1. You use this fact when you reduce fractions. If you can convert part of a given fraction into being a multiplied form of 1, then you can ignore this part, because multiplying by 1 doesn't change anying.

MathHelp.com

Reducing Fractions to Lowest Terms

For instance, here's how you would find and use a form of 1 to reduce 4/8:

$\dfrac{4}{8} = \dfrac{1 \cdot 4}{2 \cdot 4} = \dfrac{1}{2} \cdot \dfrac{4}{4} = \dfrac{1}{2} \cdot 1 = \dfrac{1}{2}$

To be very clear, the point of finding the common factor (in this case, the 4's) is to allow you to convert part of the fraction to 1. Since 4/4 = 1, then what I did above was the following:

---

Advertisement

Warning: Note how I switched from a fraction with products (in the numerator and denominator):

$\dfrac{1 \cdot 4}{2 \cdot 4}$

...to a product of fractions:

$\dfrac{1}{2} \cdot \dfrac{4}{4}$

This switch is okay as long as you're multiplying:

$\dfrac{1 \cdot 4}{2 \cdot 4} = \dfrac{1}{2} \cdot \dfrac{4}{4}$

...but it is very much NOT if you're adding. For instance:

$\dfrac{1 + 4}{2 + 4} \neq \dfrac{1}{2} + \dfrac{4}{4}$

The left-hand side above, being a fraction containing addition, is equal to 5/6, while the right-hand side above, being an addition containing fractions, is equal to 1 1/2, so the two expressions are not at all the same value. Just remember: For fractions, multiplying is way easier than adding. Now, to get back to business...

---

Content Continues Below

---

In addition to the canceling method I used above (with the pink 1's), you may also have seen either of the following "shorthands" for cancellation:

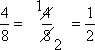
Any of these formats is fine. The last two are probably simplest for your handwritten homework; the first one is easier for typesetting.

---

If you have a regular (scientific, business, etc.) calculator that can handle fractions, then you can enter the fraction and then hit the "equals" button to get the reduced fraction. If you have a graphing calculator with a fraction command, then you can enter the fraction as a division (because 4/8 means "four divided by eight"), and then convert to fraction form. Check your manual.

If your calculator can't handle fractions, or if the denominator is too large for the calculator to handle, here's how you do the reduction by hand.

• Reduce $\mathbf{\color{green}{\dfrac{2940}{3150}}}$ to simplest form.

I'll grab my calculator and some scrap paper, and factor the numerator (top number) and denominator (bottom number). A quick shorthand for getting the prime factorization of each of these numbers is demonstrated below, in the stacked division (by prime numbers) of 2940:

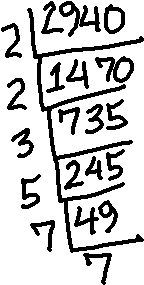
To find the factorization, I just read off the prime factors from around the outside of the upside-down division. From the above, I can see that 2940 factors as 2×2×3×5×7×7.

Affiliate

Next, I'll factor the denominator, being the number 3150:

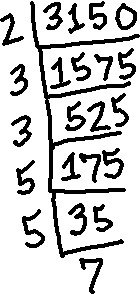
So 3150 factors as 2×3×3×5×5×7.

Now I can reduce the fraction by canceling off the common factors:

---

The next section reviews mixed numbers and improper (or "vulgar") fractions....http://www.purplemath.com/modules/fraction.htm